Sinds schooljaar 2018 – 2019 werden de scholen van het GO! via navormingen ondergedompeld in de didactiek van het ijsbergrekenen.
Vanaf september 2019 passen we deze didactiek toe in alle klasjes waar ze leren rekenen.
Hier een woordje uitleg over de ijsbergdidactiek…
Om goed te kunnen rekenen hebben kinderen veel kennis en vaardigheden nodig.
Rekenmoeilijkheden (zoals één voor één blijven tellen, omkerings- en automatiseringsmoeilijkheden) zijn meestal te wijten aan het ontbreken van de onderliggende rekenvaardigheden.
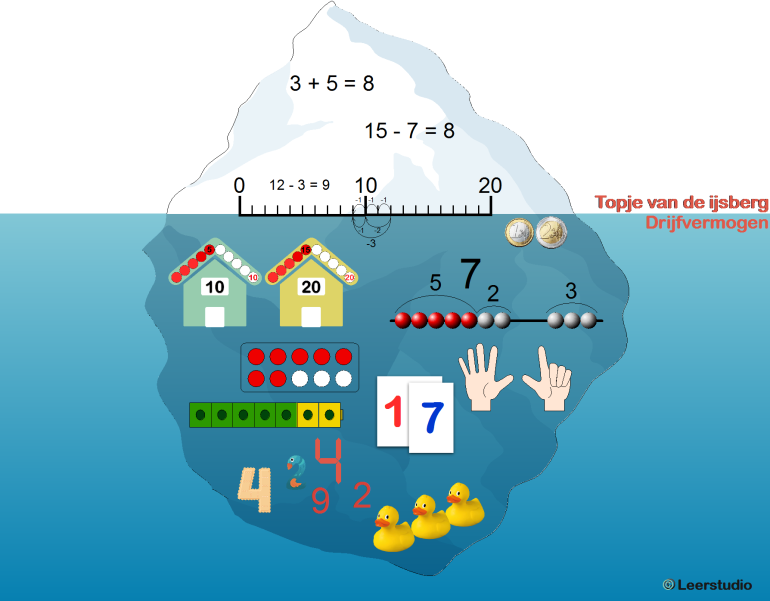
De aanpak van het ijsbergrekenen sluit nauw aan bij de basisprincipes van de rekendidactiek: van concreet, over schematisch (met een tekening) naar het abstracte formele ‘rekenen’ met getallen.
Het rekenen kan met een ijsberg worden vergeleken. Sommen zijn slechts het topje van de ijsberg. Net als bij een echte ijsberg, bevindt het belangrijkste deel zich onder de oppervlakte. Het topje komt boven door het drijfvermogen van wat onder water zit.
Sommen op papier kan je alleen begrijpen en oplossen als je kennis en veel vaardigheden hebt opgedaan. Er worden in het rekenproces vier belangrijke stappen onderscheiden die kinderen stapsgewijs moeten doorlopen om tot goed rekeninzicht te komen :
- In de eerste stap maken kinderen in een inleefbare situatie kennis met het uiterlijk en de functie van getallen, bewerkingen, verhoudingen … Wiskundige handelingen worden met concrete materialen Het materiaal is zichtbaar en telbaar.
- In de tweede stap wordt inhoud en structuuraan de werkelijkheid gegeven.
Kinderen ontdekken materialen die de concrete werkelijkheid symboliseren.
Kinderen met rekenmoeilijkheden hebben soms moeite om de overgang te maken van de concrete werkelijkheid (vader, moeder en 2 kinderen bij de bus) naar de symbolisering hiervan (bv 4 blokjes). Ze ervaren ook het voordeel van gestructureerde aantallen ten opzichte van ongestructureerde hoeveelheden.
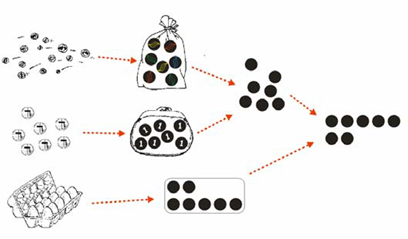
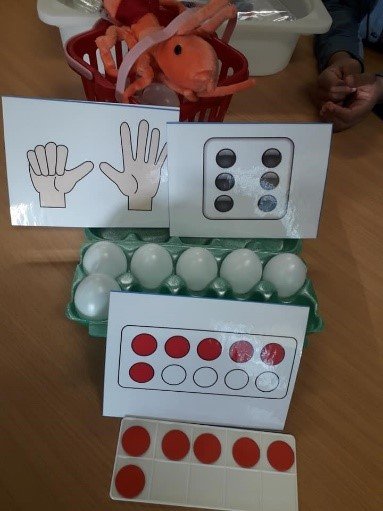
In deze fase van het leerproces doen kinderen ontdekkingen wat betreft wiskundige eigenschappen en patronen. Ze leren symbolen.
- In de derde laag wordt de werkelijkheid gerepresenteerd door getallen. Op
het niveau van getalrelaties worden de onderlinge verhoudingen tussen
getallen ontdekt. De getalbeelden zijn geautomatiseerd en hoeven niet meer
aanwezig te zijn. De getallen hebben de lading gekregen van een
gestructureerde hoeveelheid. Ze kunnen ook getallen zien als samenstellingen
van andere getallen.
- Deze drie lagen vormen samen het drijfvermogen.
- Uiteindelijk worden rekenbewerkingen in de vierde fase alleen nog met symbolen uitgebeeld. Het niveau van de formele bewerkingennoemen we de ‘top van de ijsberg’.
In deze fase vindt het automatiseren en memoriseren van sommen plaats.
Deze laatste zullen vlotter verlopen omdat ze kunnen terugvallen op hun kennis
van de bouwstenen van getallen.
